Question

Find the coordinates of C after a 90 degree clockwise rotation around the origin.

Answer 1

The answer is (0, -6)

I believe

Answer 2

Answer with explanation:

Coordinates of point C = (6,0)

Coordinates of origin, O =(0,0)

So,we have to find a segment ,perpendicular to segment O C.

Let, Coordinate of Point P,which is obtained by rotation of point C,through 90 =(x,y)

→Slope of segment O C × Slope of Segment OP,which is obtained by rotation of segment ,O C after 90°= -1

`(0-0)/(6-0) * {\text{Slope of OP}}= -1\\\\ (y-0)/(x-0)=(-6)/(0)\\\\ -6 x=0\\\\x=0`

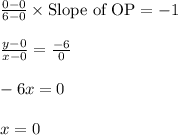
Also, OC=OP

→ O C²=O P²

∴→, x² + y²=6²

→ 0² +y²=6²

→ y²=6²

→y=6 ∧ y= -6

But we have to find point , C after a 90 degree in clockwise direction,which is = (0,-6)

Option A : (0,-6)