Answer:
x = 8
Explanation:
In the figure attached ΔABC is similar to ΔCDE
By theorem of similarity of the triangles, corresponding sides of the similar triangles will be in the same ratio.
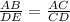
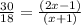
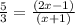
By cross multiplication
5(x + 1) = 3(2x -1)
5x + 5 = 6x - 3
5x - 6x + 5 = -3
-x + 5 = -3
-x = -3 - 5
-x = -8
x = 8
Therefore, x = 8 is the answer.