Question

Riley and Ellie go to the movie theater and purchase refreshments for their friends.

Riley spends a total of $43.00 on 2 bags of popcorn and 4 drinks.

Ellie spends a total of $14.25 on 4 bags of popcorn and 1 drink.

Write a system of equations that can be used to find the price of one bag of popcorn and the price of one drink.

Using these equations, determine and state the price of a drink, to the nearest cent.

Answer 1

2x + 4y = 43

4x + y = 14.25

1 Popcorn costs $1

1 Drink costs $10.25

Explanation:

To find the price of the popcorn and the drinks, we first need to make equations that will fit the descriptions.

Riley's Equation: 2x + 4y = $43

Ellie's Equation: 4x + y = $14.25

Let x = price of popcorn

Let y = price of drinks

Now we can find the value of x or y using the Solving Linear Equations by Multiplying First Method.

2x + 4y = 43

4x + y = 14.25

We take the first equation and multiply the whole thing by 2 to find the value of y.

2(2x + 4y = 43)

4x + 8y = 86

Now we take our new equation and subtract them to each other

4x + 8y = 86

4x + y = 14.25

7y = 71.75

Now we divide both sides by 7 to get y.

`(7y)/(7)=(71.75)/(7)`

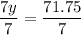
y = 10.25

Now that we have the value for y, we can then substitute the value of y in any of the two equations to find for the value of x.

2x + 4y = 43

2x + 4(10.25) = 43

2x + 41 = 43

We combine like terms and get:

2x = 43 - 41

2x = 2

Then we divide both sides by 2 to find the value of x.

`(2x)/(2)=(2)/(2)`

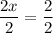
x = 1

So now that we have both values we can come to our conclusion.

1 Popcorn costs $1

1 Drink costs $10.25