Question

You work at a pioneer historical site. On this site you have handcarts. One cart has a handle that connects to the center of the wheel. We have to maintain the handle of the cart at an angle of no more than 20° with the ground so the contents do not spill out. The distance from where the handle rests on the ground to the point where the wheel is sitting on the ground is 45 inches. The distance of the center of the wheel to the end of the handle is approximately 48 inches.

a. Identify the parts of the handcart wheel that would represent congruent chords and congruent central angles. Explain why.
b. Find the radius of the wheel.
c. If the measure of the arc from to around the outside of the wheel were changed to 72°, what is the new angle the handle makes with the ground? Will the contents remain in the handcart at that angle? Will the handle rest on the ground?
d. If a pioneer pulling the handcart held the handle at a height of 48 inches off the ground, would the contents of the cart spill out the back? How high can the pioneer lift the handle off the ground before the contents started spilling out?

Answer 1

a) see below

b) radius = 16.4 in (1 d.p.)

c) 18°. Yes contents will remain. No, handle will not rest on the ground.

d) Yes contents would spill. Max height of handle = 32.8 in (1 d.p.)

Explanation:

Part a

A chord is a line segment with endpoints on the circumference of the circle.

The diameter is a chord that passes through the center of a circle.

Therefore, the spokes passing through the center of the wheel are congruent chords.

The spokes on the wheel represent the radii of the circle. Spokes on a wheel are usually evenly spaced, therefore the congruent central angles are the angles formed when two spokes meet at the center of the wheel.

Part b

The tangent of a circle is always perpendicular to the radius.

The tangent to the wheel touches the wheel at point B on the diagram. The radius is at a right angle to this tangent. Therefore, we can model this as a right triangle and use the tan trigonometric ratio to calculate the radius of the wheel (see attached diagram 1).

`\sf \tan(\theta)=(O)/(A)`

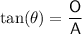
where:

• 
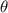  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle

Given:

• 
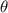  `\theta` = 20°
• O = radius (r)
• A = 45 in

Substituting the given values into the tan trig ratio:

`\implies \sf \tan(20^(\circ))=(r)/(45)`

`\implies \sf r=45\tan(20^(\circ))`

`\implies \sf r=16.37866054...`

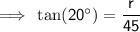
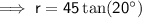
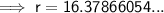
Therefore, the radius is 16.4 in (1 d.p.).

Part c

The measure of an angle formed by a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs.

If the measure of the arc AB was changed to 72°, then the other intercepted arc would be 180° - 72° = 108° (since AC is the diameter).

`\implies \sf new\: angle=(108^(\circ)-72^(\circ))/(2)=18^(\circ)`

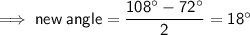
As the handle of the cart needs to be no more than 20° with the ground for the contents not to spill out, the contents will remain in the handcart at an angle of 18°.

The handle will not rest of the ground (see attached diagram 2).

Part d

This can be modeled as a right triangle (see diagram 3), with:

• height = (48 - r) in
• hypotenuse ≈ 48 in

Use the sin trig ratio to find the angle the handle makes with the horizontal:

`\implies \sf \sin (\theta)=(O)/(H)`

`\implies \sf \sin (\theta)=(48-r)/(48)`

`\implies \sf \sin (\theta)=(48-45\tan(20^(\circ)))/(48)`

`\implies \theta = 41.2^(\circ)\:\sf(1\:d.p.)`

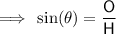
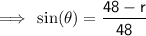
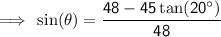
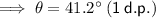
As 41.2° > 20° the contents will spill out the back.

To find the maximum height of the handle from the ground before the contents start spilling out, find the height from center of the wheel (setting the angle to its maximum of 20°):

`\implies \sin(20^(\circ))=(h)/(48)`

`\implies h=48\sin(20^(\circ))`

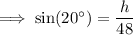
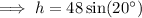
Then add it to the radius:

`\implies \sf max\:height=48\sin(20^(\circ))+45\tan(20^(\circ))=32.8\:in\:(1\:d.p.)`

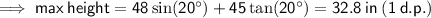
(see diagram 4)

------------------------------------------------------------------------------------------

Circle Theorem vocabulary

Secant: a straight line that intersects a circle at two points.

Arc: the curve between two points on the circumference of a circle

Intercepted arc: the curve between the two points where two chords or line segments (that meet at one point on the other side of the circle) intercept the circumference of a circle.

Tangent: a straight line that touches a circle at only one point.