Answer:
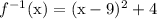 when
when
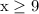
=================================================
Work Shown:
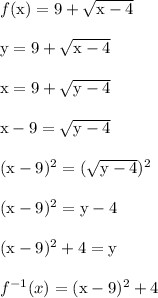
Step-by-step explanation:
I replaced f(x) with y. After that I swapped x and y, then solved for y to get the inverse.
The smallest that
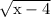 can get is 0, which means the smallest f(x) can get is 9+0 = 9. The range for f(x) is
can get is 0, which means the smallest f(x) can get is 9+0 = 9. The range for f(x) is
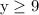
Since x and y swap to determine the inverse, the domain and range swap roles. Therefore, the domain of the inverse
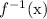 is
is
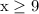
So we will only consider the right half portion of the parabola.
The graph is below. The red curve mirrors over the black dashed line to get the blue curve, and vice versa.