Answer: -√7 must also be a root of f(x).
Step-by-step explanation: Given that a polynomial function f(x) has roots 3 and radical 7.
We are to find the other number that must be a root of f(x).
We know that
irrational roots of a polynomial function always occur in conjugate pairs.
That is, if (a + √b) is a root of a polynomial function, then its conjugate pair (a - √b) is also a root of the polynomial function.
For the given polynomial f(x), the given roots are 3 and √7.
Now,
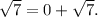
Then, the other root will be
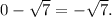
Thus, -√7 must also be a root of f(x).