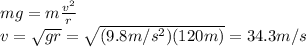Question

A car drives over a hilltop that has a radius of curvature 0.120 km at the top of the hill. At what speed would the car be traveling when it tires just barely lose contact with the road when the car is at the top of the hill?

Answer 1

34.3 m/s

Step-by-step explanation:

We can consider the car as it is in a vertical circular motion. There are two forces acting on the car:

- The weight of the car:
`mg`, where m is the mass of the car and g is the gravitational acceleration, acting downward

- The normal force exerted by the road on the car:
`N`, acting upwards

Using Newton's second law, we can write that the resultant of these two forces must be equal to the product between the mass of the car, m, and the centripetal acceleration,
`a_c`:

`mg-N=ma_c = m(v^2)/(r)`

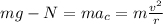
where v is the speed of the car and r = 0.120 km = 120 m is the radius of the circular trajectory.

We are asked to find the speed of the car when its tires just barely lose contact with the road: this means when the normal force exerted by the road on the car becomes zero,
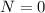`N=0`. Substituting this information into the previous equation and solving for v, we find the speed of the car:

`mg=m(v^2)/(r)\\v=√(gr)=√((9.8 m/s^2)(120 m))=34.3 m/s`