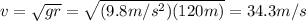Question

A car drives over a hilltop that has a radius of curvature 0.120 km at the top of the hill. At what speed would the car be traveling when it tires just barely lose contact with the road when the car is at the top of the hill?

Answer 1

34.3 m/s

Step-by-step explanation:

Newton's Second Law states that the resultant of the forces acting on the car is equal to the product between the mass of the car, m, and the centripetal acceleration
`a_c` (because the car is moving of circular motion). So at the top of the hill the equation of the forces is:

`mg-R = m a_c = m(v^2)/(r)`

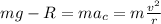
where

(mg) is the weight of the car (downward), with m being the car's mass and g=9.8 m/s^2 is the acceleration due to gravity

R is the normal reaction exerted by the road on the car (upward, so with negative sign)

v is the speed of the car

r = 0.120 km = 120 m is the radius of the curve

The problem is asking for the speed that the car would have when it tires just barely lose contact with the road: this means requiring that the normal reaction is zero, R=0. Substituting into the equation and solving for v, we find:

`v=√(gr)=√((9.8 m/s^2)(120 m))=34.3 m/s`