Question

How many ways can eight letters be arranged into groups of five where order matters and the first two letters are already chosen?

Answer 1

This problem is based on permutations because here order matters.

This problem can be found by the following solution.

When you are given 8 letters and two letters are already chosen, then 6 letters are left and you want to know in how many ways 6 letters can fill 3 spaces when order matters. So, the answer is 6P3 ways.

`(6!)/((6-3)!)`

=
`(6 *5 *4 *3 *2 *1)/(3 *2 *1)`

=
`6*5*4` = 120

Hence, there are total 120 combinations.

Answer 2

120

Explanation:

Since we're dealing with a problem where the order matters and the first two letters are already chosen we need to subtract the number of letters and the number of available slots per group.

We use the permutation formula to find the answer, but before that let's check values.

n = 8

k = 5

Now since there are two letters already chosen we have to deduct two from both the value of n and k.

n = 6

k = 3

Now we can use the permutation formula:

`_(n)P_(k)=(n!)/((n-k)!)`

`_(6)P_(3)=(6!)/(6-3)!)`

`_(6)P_(3)=(6!)/(3!)`

`_(6)P_(3)=(6*5*4*3*2*1)/(3*2*1)`

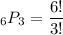
The 3*2*1 cancels out and leaves us with:

`_(6)P_(3)=6*5*4`

`_(6)P_(3)=120`

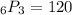
So there are 120 possible ways to arrange eight letters into groups of five where order matters and the first two letters are already chosen.