Question

Determine the number of moles in 4.75 X 1020 atoms of Lead

Answer 1

`\boxed {\boxed {\sf 7.89*10^(-4) \ mol \ Pb}}`

Step-by-step explanation:

To convert from moles to atoms, we must use Avogadro's Number. Avogadro's Number

• 6.022*10²³
• The number of particles (atoms, molcules, ions, etc.) in 1 mole.
• In this case, it is the number of atoms of lead.

1. Set up ratio

We can use Avogadro's Number as a fraction or ratio.

`(6.022*10^(23) \ atoms \ Pb)/(1 \ mol \ Pb)`

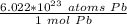
2. Convert atoms to moles

Multiply the given number of atoms by the ratio.

`4.75 *10^(20) \ atoms \ Pb *(6.022*10^(23) \ atoms \ Pb)/(1 \ mol \ Pb)`

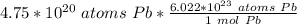
Flip the fraction so that the atoms of lead can cancel each other out.

`4.75 *10^(20) \ atoms \ Pb *(1 \ mol \ Pb)/(6.022*10^(23) \ atoms \ Pb)`

`4.75 *10^(20) *(1 \ mol \ Pb)/(6.022*10^(23) )`

`(4.75 *10^(20) \ mol \ Pb)/(6.022*10^(23) )`

`7.88774494*10^(-4) \ mol \ Pb`

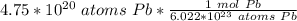
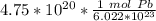
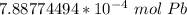
3. Round

The original measurement of 4.75 had 3 significant figures (4, 7, and 5).

We must round our answer to 3 sig figs, which is the hundredth place for the number found.

`7.88774494*10^(-4) \ mol \ Pb`

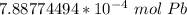
The 7 in the thousandth place tells us to round the 8 up to a 9 in the hundredth place.

`7.89*10^(-4) \ mol \ Pb`

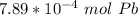
There are 7.89*10⁻⁴ moles of lead in 4.75*10²⁰ atoms of lead.