Question

Write the equation of each circle given its center and a point P that it passes through

Answer 1

(x-1)²+ (y+2)² = 25 is the equation of circle.

Explanation:

We have given the center (1,-2) and a point P (4,2) from which the circle is passes.

So, the radius of the circle is :

`r = \sqrt{(4-1)^(2)+(2-(-2))^(2)}=√(25)=5`

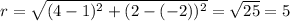
The equation of circle is :

(x - x₁)² +(y - y₁)² = r² where (x₁,y₁) is the center of circle.

Putting the value in above equation we get,

(x-1)²+(y-(-2))² = (5)²

(x-1)²+ (y+2)² = 25 is the equation of circle.

Answer 2

`(x-1)^2+(y+2)^2=25.`

Explanation:

If the center of the circle is (1,-2) and the circle passes through the point (4,2), then the radius of the circle is

`r=√((1-4)^2+(-2-2)^2)=√(9+16)=5.`

The equation of the circle with center
`(x_0,y_0)` and radius r is

`(x-x_0)^2+(y-y_0)^2=r^2.`

In your case, the equation is

`(x-1)^2+(y+2)^2=25.`