Correct answers:
- Increasing the resistivity of the material the wire is composed of will increase the resistance of the wire.
- Decreasing the cross-sectional area of the wire will increase the resistance of the wire.
- Increasing the length of the wire will increase the resistance of the wire.
Step-by-step explanation:
The resistance of a wire is given by:
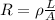
where
 is the resistitivity of the material
is the resistitivity of the material
L is the length of the wire
A is the cross-sectional area of the wire
From the formula, we can notice that:
- The resistance (R) is directly proportional to both the resistivity (
 ) and the length of the wire (L), so when one of these quantities increases, the resistance will increase as well
) and the length of the wire (L), so when one of these quantities increases, the resistance will increase as well
- The resistance (R) is inversely proportional to the cross-sectional area (A), therefore when the resistance increases when the cross-sectional area decreases.
Based on these observations, the correct statements are:
- Increasing the resistivity of the material the wire is composed of will increase the resistance of the wire.
- Decreasing the cross-sectional area of the wire will increase the resistance of the wire.
- Increasing the length of the wire will increase the resistance of the wire.