Answer:
see explanation
Explanation:
Using the trigonometric identities
• sin²x + cos²x = 1
• cot x =
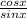 , csc x =
, csc x =
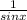
Consider the left side
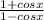 -
-

Expressing as a single fraction
=
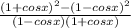
Expand and simplify numerator/ denominator
=
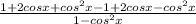
=
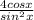
=
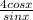 ×
×
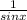
= 4cotxcscx = right side ⇒ verified