Question 1:
We have the region given by:
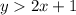
First we want to find an ordered pair that is not a solution, that is, evaluate the inequality in a pair (x, y) and that it is not fulfilled.
Example:
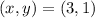
We replace:
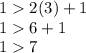
It is not fulfilled
The pair (3,1) is not a solution of
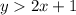
Now, we want to find an ordered pair that is a solution of the region, that is, that the inequality is met.
Example:
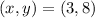
We replace:
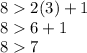
The inequality is met.
The pair (3,8) is solution of
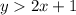
Answer:
The pair (3,1) is not a solution of
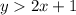
The pair (3,8) is solution of
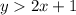
Question 2:
For this case, we must evaluate each of the options in the acad region:
Coordinate 1: (x, y) = (5,3)
Set 1:
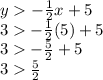
Is fulfilled.
Set 2:
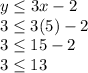
Is fulfilled.
Coordinate 2: (x, y) = (4,3)
Set 1:
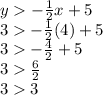
It is not fulfilled
Set 2:
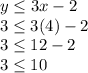
If it is fulfilled.
Coordinate 3: (x, y) = (3,4)
Set 1:
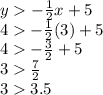
It is not true
Set 2:
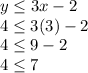
Is fulfilled.
Coordinate 4: (x, y) = (4,4)
Set 1:
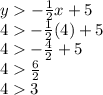
It is not true
Region 2:
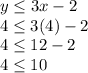
Is fulfilled
Answer:
There is not a pair that is not a solution of both at the same time