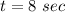Question

A ball is thrown into the air from a height of 256 feet at time t=0. The function that models this situation is h(t)=-16t^2 + 96t + 256, where t is in seconds and h is the height in feet.

A.) what is the height of the ball at 2 seconds?
B.) When will the ball reach a height of 144 feet?
C.) When will the ball hit the ground?

Answer 1

Part A) The height of the ball at 2 seconds is
`384\ ft`

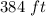
Part B)
`t=7\ sec`

Part C)
`t=8\ sec`

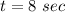
Explanation:

Part A) what is the height of the ball at 2 seconds?

we have

`h(t)=-16t^(2) +96t+256`

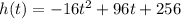
so

For
`t=2\ sec`

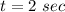
Substitute the value of t in the equation and solve for h

`h(2)=-16(2^(2)) +96(2)+256`

`h(2)=384\ ft`

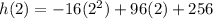
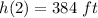
Part B) When will the ball reach a height of 144 feet?

Substitute the value of
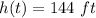`h(t)=144\ ft` in the equation and solve for t

so

`144=-16t^(2) +96t+256`

`-16t^(2) +96t+112=0`

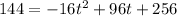
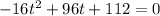
we know that

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`-16t^(2) +96t+112=0`

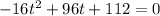
so

`a=-16\\b=96\\c=112`

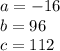
substitute in the formula

`t=\frac{-96(+/-)\sqrt{96^(2)-4(-16)(112)}} {2(-16)}`

`t=\frac{-96(+/-)√(16,384)} {-32}`

`t=\frac{-96(+/-)128} {-32}`

`t=\frac{-96(+)128} {-32}=-1`

`t=\frac{-96(-)128} {-32}=7`

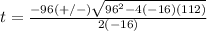
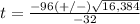
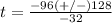
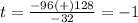
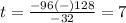
therefore

the solution is the positive value

`t=7\ sec`

Part C) When will the ball hit the ground?

Substitute the value of
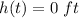`h(t)=0\ ft` in the equation and solve for t

so

`0=-16t^(2) +96t+256`

`-16t^(2) +96t+256=0`

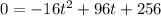
we know that

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`-16t^(2) +96t+256=0`

so

`a=-16\\b=96\\c=256`

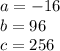
substitute in the formula

`t=\frac{-96(+/-)\sqrt{96^(2)-4(-16)(256)}} {2(-16)}`

`t=\frac{-96(+/-)√(25,600)} {-32}`

`t=\frac{-96(+/-)160} {-32}`

`t=\frac{-96(+)160} {-32}=-2`

`t=\frac{-96(-)160} {-32}=8`

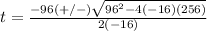
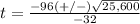
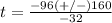
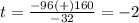
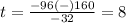
therefore

the solution is the positive value

`t=8\ sec`