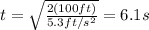Question

On the Moon, acceleration resulting from gravity, g, is about 5.3 ft/s2. Which expression gives the time, in seconds, it would take a dropped penny to fall 100 ft on the Moon?

Answer 1

`20\sqrt[]{5/53}`

Answer 2

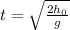`t=\sqrt{(2h_0)/(g)}`, 6.1 s

Step-by-step explanation:

The motion of the dropped penny is a uniformly accelerated motion, with constant acceleration

`g=5.3 ft/s^2`

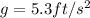
towards the ground. If the penny is dropped from a height of

`h_0 = 100 ft`

the vertical position of the penny at time t is given by the equation

`h(t) = h_0 - (1)/(2)gt^2`

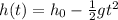
where the negative sign is due to the fact that the direction of the acceleration is downward.

We want to know the time t at which the penny reaches the ground, which means h(t)=0. Substituting into the equation, it becomes

`0=h_0 - (1)/(2)gt^2`

And re-arranging it, we find an expression for the time t:

`t=\sqrt{(2h_0)/(g)}`

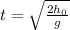
And substituting the numbers, we can also find the numerical value:

`t=\sqrt{(2(100 ft))/(5.3 ft/s^2)}=6.1 s`