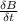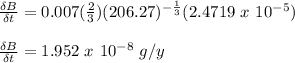Answer:

Explanation:
We need to know how fast the brain of the species grows at the point where its average length was 19 cm.
In other words we need to find:
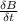
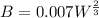
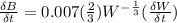
Now we need to find
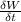
In the statement of the problem it is said that
 is constant.
is constant.
It is also said that the length changed from 14 to 23 cm in
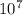 years.
years.
So:
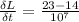
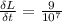
Now we find
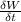

Now we find W and
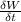 for L = 19
for L = 19


Now replace
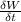 and W in the main equation of
and W in the main equation of