Answer: 3 seconds
We are given the following function:
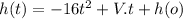 (1)
(1)
Where:
 is the time the ball is in the air
is the time the ball is in the air
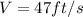 the initial upward velocity
the initial upward velocity
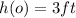 the initial height of the ball
the initial height of the ball
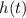 is the final height of the ball. If no one catches it, this will be zero
is the final height of the ball. If no one catches it, this will be zero
So, equation (1) changes to:
 (2)
(2)
Substituting the known values:
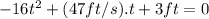 (3)
(3)
This is a quadratic equation in the form
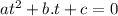 . In order to find
. In order to find
 we can use the quadratic formula for the roots:
we can use the quadratic formula for the roots:
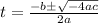 (4)
(4)
Where
 ,
,
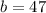 and
and
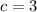
Substituting this values in (4):
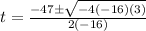 (5)
(5)
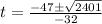 (6)
(6)
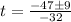 (7)
(7)
For
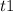 :
:
 (8)>>>> This result does not work for us because is negative
(8)>>>> This result does not work for us because is negative
For
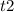 :
:
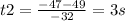 (9)>>>This is the result
(9)>>>This is the result
Therefore:
If no one catches the ball, it will be 3 s in the air