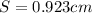For this case, the first thing you should know is that the formula for the arc length is given by:
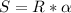
Where,
- R: radius of the circle
- α: central angle.
For this case we are going to assume that the correct data are:
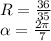
Substituting values we have:
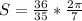
Calculated:
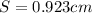
Answer:
The arc length is: