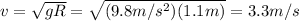Question

A tennis ball connected to a string is spun around in a vertical, circular path at a uniform speed. The ball has a mass m = 0.158 kg and moves at v = 5.22 m/s. The circular path has a radius of R = 1.1 m 1) What is the magnitude of the tension in the string when the ball is at the bottom of the circle? 2) What is the magnitude of the tension in the string when the ball is at the side of the circle? . 3) What is the magnitude of the tension in the string when the ball is at the top of the circle? 4) What is the minimum velocity so the string will not go slack as the ball moves around the circle?

Answer 1

1) 5.5 N

When the ball is at the bottom of the circle, the equation of the forces is the following:

`T-mg = m(v^2)/(R)`

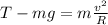
where

T is the tension in the string, which points upward

mg is the weight of the string, which points downward, with

m = 0.158 kg being the mass of the ball

g = 9.8 m/s^2 being the acceleration due to gravity

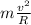`m (v^2)/(R)` is the centripetal force, which points upward, with

v = 5.22 m/s being the speed of the ball

R = 1.1 m being the radius of the circular trajectory

Substituting numbers and re-arranging the formula, we find T:

`T=mg+m(v^2)/(R)=(0.158 kg)(9.8 m/s^2)+(0.158 kg)((5.22 m/s)^2)/(1.1 m)=5.5 N`

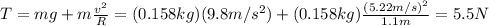
2) 3.9 N

When the ball is at the side of the circle, the only force acting along the centripetal direction is the tension in the string, therefore the equation of the forces becomes:

`T=m(v^2)/(R)`

And by substituting the numerical values, we find

`T=(0.158 kg)((5.22 m/s)^2)/(1.1 m)=3.9 N`

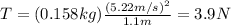
3) 2.3 N

When the ball is at the top of the circle, both the tension and the weight of the ball point downward, in the same direction of the centripetal force. Therefore, the equation of the force is

`T+mg=m(v^2)/(R)`

And substituting the numerical values and re-arranging it, we find

`T=m(v^2)/(R)-mg=(0.158 kg)(5.22 m/s)^2)/(1.1 m)-(0.158 kg)(9.8 m/s^2)=2.3 N`

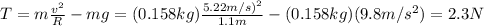
4) 3.3 m/s

The minimum velocity for the ball to keep the circular motion occurs when the centripetal force is equal to the weight of the ball, and the tension in the string is zero; therefore:

`T=0\\mg = m(v^2)/(R)`

and re-arranging the equation, we find

`v=√(gR)=√((9.8 m/s^2)(1.1 m))=3.3 m/s`