Question

Given: X = r + 2, Y = 2r - 9, and Z = r 2 + 17r + 30. Simplify [X · Y - Z] ÷ X. -r - 24 r - 24 2r2 - 6r - 33 2r2 + 6r + 33

Answer 1

r - 24

Explanation:

Use PEMDAS:

P Parentheses first

E Exponents (ie Powers and Square Roots, etc.)

MD Multiplication and Division (left-to-right)

AS Addition and Subtraction (left-to-right)

================================================

`X=r+2,\ Y=2r-9,\ Z=r^2+17r+30`

`[X\cdot Y-Z]/ X`

First: the product X · Y:

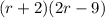`(r+2)(2r-9)` use FOIL (a + b)(c + d) = ac + ad + bc + bd

`=(r)(2r)+(r)(-9)+(2)(2r)+(2)(-9)\\\\=2r^2-9r+4r-18=2r^2+(-9r+4r)-18\\\\=2r^2-5r-18`

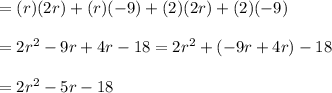
Second: the difference X · Y - Z:

`2r^2-5r-18-(r^2+17r+30)=2r^2-5r-18-r^2-17r-30\\\\=(2r^2-r^2)+(-5r-17r)+(-18-30)\\\\=r^2-22r-48`

Third: the quotient [X · Y - Z] ÷ X:

`(r^2-22r-48)/(r+2)=(r^2-22r-48)/(r+2)=(r^2+2r-24r-48)/(r+2)\\\\=(r(r+2)-24(r+2))/(r+2)=((r+2)(r-24))/(r+2)`

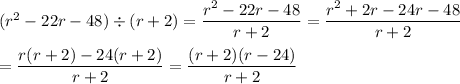
cancel r + 2

`=r-24`

Answer 2

r - 24

Explanation:

[X · Y - Z] = (r + 2)(2r - 9)] - (r^2 + 17r + 30)

= (2r^2 + 4r - 9r - 18 ) - r^2 - 17r - 30

= 2r^2 - 5r - 18 - r^2 - 17r - 30

= r^2 - 22r - 48

= (r +2)(r - 24)

so

[X · Y - Z] / X

= [(r +2)(r - 24)] / (r + 2)

= r - 24