Question

What is the perimeter of ΔBDE?

a) √17 + √26 + 5
b) 4 √2 + √65 + 5
c) √34 + √65 + 5
d) √17 + 4 √7 + 2 √3

Answer 1

a)
`\displaystyle √(17) + √(26) + 5`

Step-by-step Step-by-step explanation:

To find the length of all three sides, you have to use the Distance Formula:

`\displaystyle √([-x_1 + x_2]^2 + [-y_1 + y_2]^2) = D`

D[2, 6], and B[−2, 3] → DB

`\displaystyle √([-2 - 2]^2 + [-6 + 3]^2) = √([-4]^2 + [-3]^2) = √(16 + 9) = √(25) = 5`

DB is 5 units long.

E[3, 2] and B[−2, 3] → EB

`\displaystyle √([-3 - 2]^2 + [-2 + 3]^2) = √([-5]^2 + 1^2) = √(25 + 1) = √(26)`

EB is
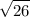`\displaystyle √(26)`units long.

E[3, 2] and D[2, 6] → ED

`\displaystyle √([-3 + 2]^2 + [-2 + 6]^2) = √([-1]^2 + 4^2) = √(1 + 16) = √(17)`

ED is
`\displaystyle √(17)`units long.

Altogether, you have the perimeter of
`\displaystyle √(17) + √(26) + 5`units.

I am joyous to assist you anytime.

* Since we are talking about distance, we ONLY want the NON-NEGATIVE roots.