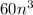Question

Thanks guys for the help. This one and one more and I’m done!

Answer 1

60n³

Explanation:

The least common multiple of two expressions is the value of the lowest common coefficient and variable exponent. In this case, look first at the coefficent:

12: 12, 24, 36, 48, 60

15: 15, 30, 45, 60

So, the least common coefficient is 60.

Next, look at the exponents of the variable:

n: n, n², n³

n³: n³

The combined term would be: 60n³

Answer 2

Answer:
`60n^(3)`

Explanation:

To find the least common multiply, you must descompose 12 and 15 into their prime factors, as you can see below:

12=2*2*3=2²*3

15=3*5

Choose the common and non common numbers with their greastest exponents:

3*5*2²=60

Now you must choose the common and non common variables with their greastest exponents:

n³

Therefore, you can conclude that the least common multiply is:

`60n^(3)`