Question

What are the steps to converting a function from standard form to vertex form?

Answer 1

1) Identify the values of a, b and c in the function
`f(x) = ax ^ 2 + bx + c`

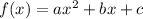
2) Do
`x = -(b)/(2a)`

`y = f(-(b)/(2a))`

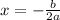
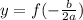
3) Then
`h = x` and
`k = y`

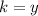
4) Once found the values of h and k, write the equation as:

`f(x) = (x-h) ^ 2 + k`

Explanation:

The standard form of a quadratic function is:

`f(x) = ax ^ 2 + bx + c`

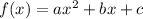
Where a, b and c are the coefficients of the monomials, and they are real numbers. By definition, the vertex of this function is:

`(-(b)/(2a), f(-(b)/(2a)))`

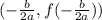
Then, the vertex form of a quadratic function is:

`f(x) = (x-h) ^ 2 + k`

Where the point (h, k) represents the vertex of the function.

The steps to convert a quadratic function to the standard form the vertex form is:

1) Identify the values of a, b and c in the function
`f(x) = ax ^ 2 + bx + c`

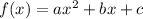
2) Do
`x = -(b)/(2a)`

`y = f(-(b)/(2a))`

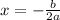
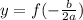
3) Then
`h = x` and
`k = y`

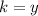
4) Once found the values of h and k, write the equation as:

`f(x) = (x-h) ^ 2 + k`