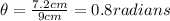Answer: 0.8 radians
Explanation:
To solve this exercise you must apply the formula shown below:
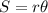
Where S is the arc lenght, r is the radius of the circle and
 is the central angle in radians.
is the central angle in radians.
Solve for the central angle:
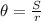
Now, when you susbtitute the value of the arc length and the radius, you obtain that the central angle is: