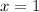Question

HElP
!!!!!!!!!!!’nnnnnnnnnnn

Answer 1

1

Explanation:

1.000000

Answer 2

x = 1

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Equality Properties

Algebra II

• Logarithms
• Solving Exponentials

Explanation:

Step 1: Define

`\displaystyle 2^(x+4) - 12 = 20`

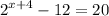
Step 2: Solve for x

1. Isolate x term:
   `\displaystyle 2^(x+4) = 32`
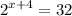
2. Rewrite 32:
   `\displaystyle log_2(32) = 5`
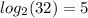
3. Rewrite equation:
   `\displaystyle 2^(x+4) = 2^5`
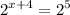
4. Set equal:
   `\displaystyle x + 4 = 5`
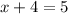
5. Isolate x:
   `\displaystyle x = 1`