Question

How do you find the perimeter of a parallelogram​

Answer 1

• There may be a simpler way to solve this question, however if you are currently learning distance formula, then this may be the correct way to solve it.

Answer: D

Explanation:To find the perimeter of this parallelogram, you would have to find the distance between the coordinates.

I would use the distance formula for this question.

Distance Formula -
`d=\sqrt{(x_2 -x_1)^(2)+(y_2 -y_1)^(2)}`

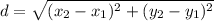
Ok, let's find the length of side AB.

Coordinates of A = (-5, -7) This will be our second x and y coordinates [
`x_2,y2`]

Coordinates of B = (2, -3) These will be our first x and y coordinates [
`x_1,y1`]

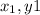Now Substitute Into The Equation -

`d=\sqrt{(-5-2)^(2) +(-7-(-3))^(2) }`

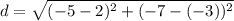
Solve/Simplify -

`√((-5-2)^2+(-7-(-3))^2) \\ \\ √((-5-2)^2+(-7+3)^2) \\\\√((-7)^2+(-4)^2)\\\\ √(49+16) \\\\ √(65)`

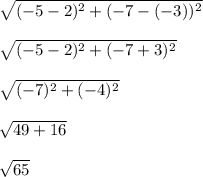
• Great! We have the first distance for the perimeter.

Now let's solve for side CB

Point C = (-1, 2) This will be our second x and y coordinates [
`x_2,y2`]

Point B = (2, -3) These will be our first x and y coordinates [
`x_1,y1`]

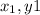Substitute and Solve -

`√((-1-2)^2+(2-(-3))^2)\\\\sqrt{(-1-2)^2+(2+3)^2}\\\\\ √((-3)^2+(5)^2)\\\\ √(9+25)\\\\√(34)`

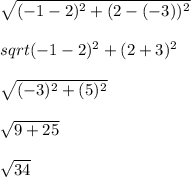
• Now we have our second distance for the perimeter.

Now solve for the other two sides -

Because this shape is a rectangle, the parallel lines are the same length.

Now, find the perimeter-

`√(65)+ √(65)+ √(34) +√(34)`

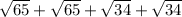
• That equals about 27.79, rounding up to 27.8

Hoped this helped!~