Question

A sequence consists of the positive odd integers. What is the sum of the first 12 terms of the sequence?

A. 144
B. 169
C. 115
D. 121

Answer 1

A

Explanation:

The sequence of positive odd numbers is

1, 3, 5, 7, ......

This is an arithmetic sequence with common difference d

d = 3 - 1 = 5 - 3 = 7 - 5 = 2

The sum to n terms of an arithmetic sequence is

`S_(n)` =
`(n)/(2)`[2a + (n - 1)d ]

where a is the first term

here a = 1, d = 2, n = 12, hence

`S_(12)` =
`(12)/(2)`[1 + (11 × 2) ]

= 6 [ 2 + (11 × 2) ]

= 6 × 24 = 144 → A

Answer 2

A. 144.

Explanation:

We have been given that a sequence consists of the positive odd integers. We are asked to find the sum of the first 12 terms of the sequence.

Our sequence would be: 1, 3, 5, 7, 9, 11, ....,

We will use sum of sequence formula to solve our given problem.

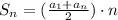`S_n=((a_1+a_n)/(2))\cdot n`, where,

`a_1` = 1st term of sequence,

`a_n` = nth term of sequence,

`n` = Number of terms is the sequence.

Let us find nth term of sequence using formula:

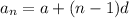`a_n=a+(n-1)d`, where,

d = Difference between two consecutive terms of sequence.

`d=3-1=2`

`a_n=1+(12-1)2`

`a_n=1+(11)2`

`a_n=1+22`

`a_n=23`

`S_n=((1+23)/(2))\cdot 12`

`S_n=24\cdot 6`

`S_n=144`

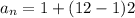
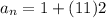
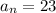
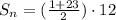
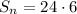
Therefore, the sum of 1st 12 terms of the sequence is 144 and option A is the correct choice.