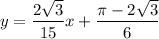Question

Find the equation of the line tangent to the graph of

y = sin^-1 (x/5) at x = 5/2. Show your work.

Answer 1

`\displaystyle y=(2√(3))/(15)x+(\pi-2√(3))/(6)`

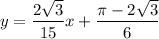
Explanation:

We want to find the equation of the line tangent to the graph of:

`\displaystyle y=\sin^(-1)\left((x)/(5)\right)\text{ at } x=(5)/(2)`

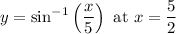
So, we will find the derivative of our equation first. Applying the chain rule, we acquire that:

`\displaystyle y^\prime=\frac{1}{\sqrt{1-\left((x)/(5)\right)^2}}\cdot(1)/(5)`

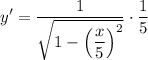
Simplify:

`\displaystyle y^\prime=\frac{1}{5\sqrt{1-(x^2)/(25)}}`

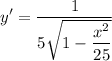
We can factor out the denominator within the square root:

`\displaystyle y^\prime =\frac{1}{5\sqrt{(1)/(25)\big(25-x^2)}}`

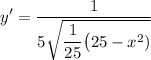
Simplify:

`\displaystyle y^\prime=(1)/(√(25-x^2))`

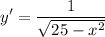
So, we can find the slope of the tangent line at x = 5/2. By substitution:

`\displaystyle y^\prime=(1)/(√(25-(5/2)^2))`

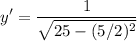
Evaluate:

`\displaystyle y^\prime=(1)/(√(75/4))=(1)/((5√(3))/(2))=(2√(3))/(15)`

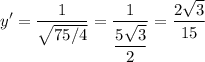
We will also need the point at x = 5/2. Using our original equation, we acquire that:

`\displaystyle y=\sin^(-1)\left((1)/(2)\right)=(\pi)/(6)`

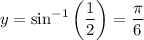
So, the point is (5/2, π/6).

Finally, by using the point-slope form, we can write:

`\displaystyle y-(\pi)/(6)=(2√(3))/(15)\left(x-(5)/(2)\right)`

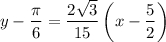
Distribute:

`\displaystyle y-(\pi)/(6)=(2√(3))/(15)x+(-√(3))/(3)`

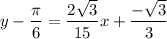
Isolate. Hence, our equation is:

`\displaystyle y=(2√(3))/(15)x+(\pi-2√(3))/(6)`