Question

using the graph of f(x)=1/× as a guide describe the transformation and graph the function g(x)=2/x+4​

Answer 1

A transformed function of f(x) is defined as,

g(x) = k f(x+a) + b,

Where k shows the stretch or compression ( When |k| > 1 or 0 < |k| < 1 ),

a shows the horizontal shifting, ( When a > 0 then it is shifted left when a < 0 then it is shifted right)

b shows the vertical shifting. ( b > 0 then it is shifted up b < 0 then it is shifted down)

Here, the parent function is,

`f(x) = (1)/(x)`

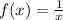
And, transformed function is,

`g(x) = (2)/(x+4)= 2f(x+4)`

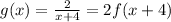
Thus, by the above explanation,

g(x) is obtained after shifting of f(x) horizontally left by 4 unit and after stretched by 2 unit.