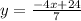The question is incomplete.
However, from the given parameters, a likely question could be to:
1. Write an equation in slope intercept form through (20,-8) and is parallel to 7x - 4y = -5
or
2. Write an equation in slope intercept form through (20,-8) and is perpendicular to 7x - 4y = -5
Answer:
See Explanation
Explanation:
First, we calculate the slope of
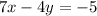
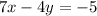
Subtract 7x from both sides
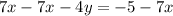
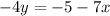
Make y the subject
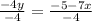
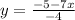
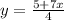
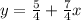
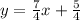
The general format of an equation is:
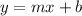
Where
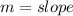
By comparison:

Solving (1): Parallel
Here, we assume that the line is parallel to the given equation.
And as such, it means that they have the same slope
So, we have:
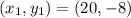
and

The equation is then calculated as:

This gives:
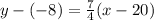
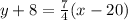
Open bracket
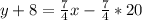
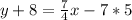
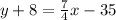
Make y the subject
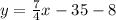
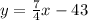
Solving (2): Perpendicular
Here, we assume that the line is perpendicular to the given equation.
And as such, it means that the following relationship exists between their slope:
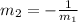
Where
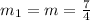 -- as calculated above
-- as calculated above
Substitute 7/4 for m1 in
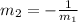
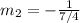
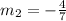
So, we have:
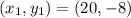
and
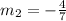
The equation is then calculated as:

This gives:
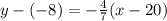
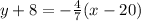
Open bracket
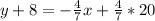

Make y the subject
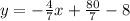
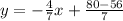
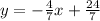
Take LCM