Question

Consider the quadratic function y = 1/5

(x – 2)2 + 5. Which statements are true about the function and its graph? Check all that apply. The vertex of the function is (–2, 5). There are no real roots for the function. The graph of the function opens down. The graph contains the point (2, 5). The graph intersects the x-axis at one unique point.

Answer 1

Answers:

We have the quadratic function:

`y=(1)/(5)(x-2)^2+5\\y=(x^2)/(5)-(4x)/(5)+(4)/(5)+5\\y=(x^2)/(5)-(4x)/(5)+(29)/(5)`

• The vertex of the function is (-2,5):

A quadratic function has the form:
`ax^2+bx+c` where
`a\\eq 0`

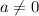
The vertex is the lowest or the highest point of the parabola. The formula of the vertex is:

`x=-(b)/(2a)`

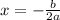
We have
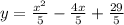`y=(x^2)/(5)-(4x)/(5)+(29)/(5)` where

`a=(1)/(5) \\b=-(4)/(5) \\c=(29)/(5)`

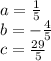
then the vertex is:

`x=-(((-4))/(5) )/(2(1)/(5))\\\\x=((4)/(5))/((2)/(5))\\\\x=2`

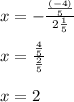
Now we have to replace x=2 in

`y=(x^2)/(5)-(4x)/(5)+(29)/(5)\\\\y=((2)^2)/(5)-(4.(2))/(5)+(29)/(5)\\\\y=(4)/(5)-(8)/(5)+(29)/(5)\\\\y=(25)/(5)\\\\y=5`

Then the vertex of the parabola is in the point (2,5).

The statement "The vertex of the function is (-2,5)" is False.

• There are no real roots for the function:

The roots of a quadratic function are the ones that meet that y=0.

This means

`y=(x^2)/(5)-(4x)/(5)+(29)/(5)=0\\(x^2)/(5)-(4x)/(5)+(29)/(5)=0`

We are going to use Baskhara's Formula:
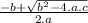`\frac{-b+\sqrt{b^(2)-4.a.c} }{2.a}` and
`\frac{-b-\sqrt{b^(2)-4.a.c} }{2.a}`

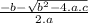
Replacing a, b and c :

`x_(1)= \frac{-((-4))/(5) +\sqrt{(-4)^(2)-4.(1)/(5) .(29)/(5) } }{2.(1)/(5)}\\\\x_(1)=\frac{(4)/(5) +\sqrt{16-(116)/(5) } }{(2)/(5) }`

`x_(2)= \frac{-((-4))/(5) -\sqrt{(-4)^(2)-4.(1)/(5) .(29)/(5) } }{2.(1)/(5)}\\\\x_(2)=\frac{(4)/(5) -\sqrt{16-(116)/(5) } }{(2)/(5) }`

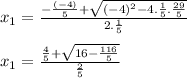
We can see that
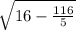`\sqrt{16-(116)/(5) }`<0 this means that there aren't real solutions.

Then the statement "There are no real roots for the function" is True.

• The graph of the function opens down:

A quadratic function has the form:
`ax^2+bx+c` where
`a\\eq 0` and if a>0 the parabola opens up, if a<0 the parabola opens down.

In this case
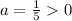`a=(1)/(5) >0` then the parabola opens up.

The statement "The graph of the function opens down" is False.

• The graph contains the point (2, 5):

To see if the graph contains the point we have to see if it verifies the equation of the quadratic function:

`y=(x^2)/(5)-(4x)/(5)+(29)/(5)`

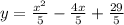
We have to replace x=2 and y=5

`y=(x^2)/(5)-(4x)/(5)+(29)/(5)\\\\5=(2^2)/(5)-(4.2)/(5)+(29)/(5)\\\\5=(4)/(5)-(8)/(5)+(29)/(5)\\\\5=(25)/(5)\\\\5=5`

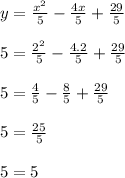
Is verified. Then the point (2,5) is in the graph of the function.

The statement "The graph contains the point (2, 5)" is True.

Also you can see that this point is the vertex of the parabola.

• The graph intersects the x-axis at one unique point:

We saw that the equation doesn't have real roots, this means that the graph doesn't intersects the x-axis.

Then the statement "The graph intersects the x-axis at one unique point" is False.

The graph of the function is:

Answer 2

There are no real roots for the function. TRUE

The graph contains the point (2, 5). TRUE

Explanation:

For the quadratic function
`y = (1)/(5)(x-2)^2 + 5` it has vertex (2, 5). Its graph is attached. Since it opens up above the x-axis, it has no x-intercepts and therefore no real roots.

The following are true or false:

The vertex of the function is (–2, 5). FALSE

There are no real roots for the function. TRUE

The graph of the function opens down. FALSE

The graph contains the point (2, 5). TRUE

The graph intersects the x-axis at one unique point. FALSE