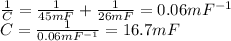Question

What is the total capacitance in units of mF, of the two capacitors connected in series, as shown in the diagram, when C1 = 45 mF and C2 = 26 mF?

Answer 1

The total capacitance will be 16.12mF

Step-by-step explanation:

The total capacitance in series is calculated by

1/Ct = 1/C1 + 1/C2 + 1/C3 .........

1/Ct = 1/ 45 + 1/26

1/Ct = 0.022 + 0.04

1/Ct = 0.062

Ct = 16.12mF

Answer 2

16.7 mF

Step-by-step explanation:

The total capacitance of two capacitors connected in series is given by the formula:

`(1)/(C)=(1)/(C_1)+(1)/(C_2)`

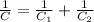
in our problem, we have:

C1 = 45 mF is the capacitance of the first capacitor

C2 = 26 mF is the capacitance of the second capacitor

Substituting into the equation, we find:

`(1)/(C)=(1)/(45 mF)+(1)/(26 mF)=0.06 mF^(-1)\\C=(1)/(0.06 mF^(-1))=16.7 mF`