Question

Use the definition of continuity to determine whether f is continuous at a. f(x) = 5x+5 a = -5 Question

Answer 1

f is continuous at a = -5.

Explanation:

We have given a function.

f(x) = 5x+5

We have to check continuity of function at a = -5.

From definition of continuity,

If f is continuous at x = a

`\lim_(x \to a) f(x)= f(a)`

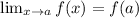
Putting x = a = -5 in given function ,we have

f(-5) = 5(-5)+5 = -25+5

f(-5) = -20

`\lim_(x\to-5) f(x) =5(-5)+5`

`\lim_(x \to-5)f(x) = -20`

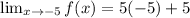
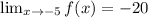
Hence,
`\lim_(x \to-5) f(x)= f(-5)`

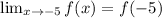
f is continuous at a = -5.

Answer 2

`lim_(x \to - 5)(f(x)) = f( - 5)`

EXPLANATION

If f(x) is continuous at

`x = a`

Then,

`lim_(x \to a)(f(x)) = f(a)`

The given function is

`f(x) = 5x + 5`

`f( - 5) = 5( - 5) + 5`

`f( - 5) = - 25 + 5 = - 20`

`lim_(x \to - 5)(f(x)) = 5( - 5) + 5`

`lim_(x \to - 5)(f(x)) = - 20`

Since,

`lim_(x \to - 5)(f(x)) = f( - 5)`

The function is continuous at

`x = - 5`