(a) f = 5.00 × 10²⁰ Hz, E = 3.32 × 10⁻¹³ J;
(b) f = 1.20 × 10¹⁰ Hz, E = 7.96 × 10⁻²⁴J.
Step-by-step explanation
What's the similarity between a gamma ray and a microwave?
Both gamma rays and microwave rays are electromagnetic radiations. Both travel at the speed of light at
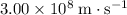 in vacuum.
in vacuum.
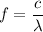
where
- f is the frequency of the electromagnetic radiation,
- c is the speed of light, and
 is the wavelength of the radiation.
is the wavelength of the radiation.
(a)
Convert all units to standard ones.
 .
.
The unit of
 shall also be standard.
shall also be standard.
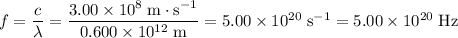 .
.
For each particle,
 ,
,
where
 is the energy of the particle,
is the energy of the particle,
 is the planck's constant where
is the planck's constant where
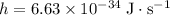 , and
, and
 is the frequency of the particle.
is the frequency of the particle.
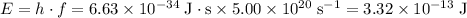 .
.
(b)
Try the steps in (a) for this beam of microwave with
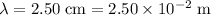 .
.
Expect the following results:
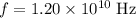 , and
, and
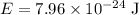 .
.