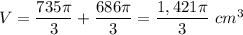Answer:

Explanation:
We have the cone and the half-sphere.
The formula of a volume of a cone:
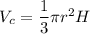
r - radius
H - height
We have r = 7cm and H = (22-7)cm=15cm. Substitute:
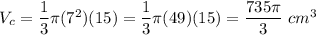
The formula of a volume of a sphere:
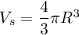
R - radius
Therefore the formula of a volume of a half-sphere:
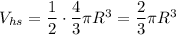
We have R = 7cm. Substitute:
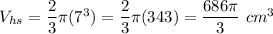
The volume of the given shape:
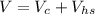
Substitute: