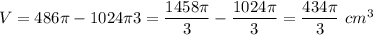Question

A hemispherical wooden bowl has an internal radius of 8cm and an external radius of 9cm

Calculate the volume of the wood​

Answer 1

454.5 cm³

Explanation:

The volume (V) of a sphere is calculated using formula

V=
`(4)/(3)`πr³ ← r is the radius

Thus the volume (V) of a hemisphere is

V =
`(1)/(2)` ×
`(4)/(3)`πr³ =
`(2)/(3)`πr³

`V_(wood)` =
`V_(external)` -
`V_(internal)`

=
`(2)/(3)`π × 9³ -
`(2)/(3)`π × 8³

=
`(2)/(3)`π (9³ - 8³)

=
`(2)/(3)`π (729 - 512 )

=
`(2)/(3)`π × 217 ≈ 454.5 cm³

Answer 2

`\large\boxed{V=(434\pi)/(3)\ cm^3}`

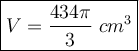
Explanation:

We have a hemisphere with a radius 9 cm with a hemisphere cut out with radius 8cm.

Calculate a volume of a larger hemisphere and subtract from it a volume of smaller hemisphere.

The formula of a volume of a sphere:

`V_s=(4)/(3)\pi R^3`

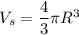
R - radius

Therefore the formula of a volume of a hemisphere:

`V_(hs)=(1)/(2)\cdot(4)/(3)\pi R^3=(2)/(3)\pi R^3`

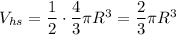
The volume of the larger hemisphere:

`V_l=(2)/(3)\pi(9^3)=(2)/(3)\pi(729)=(2)(\pi)(243)=486\pi\ cm^3`

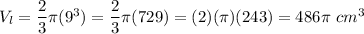
The volume of the smaller hemisphere:

`V_s=(2)/(3)\pi(8^3)=(2)/(3)\pi(512)=(1024\pi)/(3)\ cm^3`

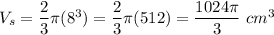
The volume of wood:

`V=V_l-V_s`

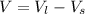
Substitute:

`V=486\pi-\dfac{1024\pi}{3}=(1458\pi)/(3)-(1024\pi)/(3)=(434\pi)/(3)\ cm^3`