Question

How to do this? (#21 and #23)

The graph of g is a transformation of the graph of f. Write a rule for g. ​

Answer 1

`\large\boxed{21.\ g(x)=f(x-2)+1\to g(x)=\log_3(x-2)+1}\\\\\boxed{22.\ g(x)=f(x)-4\to g(x)=3^x-4}\\\\\boxed{23.\ g(x)=-f(x)\to g(x)=-\log_{(1)/(2)}x}`

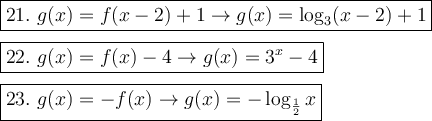
Explanation:

f(x) + n - shift the grapf n units up

f(x) - n - shift the grapf n units down

f(x + n) - shift the grapf n units to the left

f(x - n) - shift the grapf n units to the right

-f(x) - reflection about the x-axis

f(-x) - reflection about the y-axis

============================================

Look at the picture.

`21.\\f(x)=\log_3x\\\\g(x)=\log_3(x-2)+1`

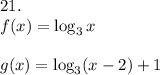
move the graph 2 units to the right and 1 unit up

`22.\\f(x)=3^x\\\\g(x)=3^x-4`

move the graph 4 units down

`23.\\f(x)=\log_{(1)/(2)}x\\\\g(x)=-\log_{(1)/(2)}x`

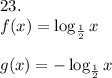
reflection the graph about the X axis.

Answer 2

21. g(x) = f(x-1); 23. g(x) = -ƒ(x)

Explanation:

21. ƒ(x) = log₃x

The graph is shifted one unit to the right.

One unit must have been subtracted from x.

g(x) = -f(x-1) = log₃(x-1)

Figure 1 shows ƒ(x) (blue) and g(x) (green) shifted one unit to the right,

23.
`f(x) = \log_{(1 )/( 2)}x`

The graph is inverted.

ƒ(x) must have been multiplied by -1.

g(x) = -ƒ(x)

`g(x) = -\log_{(1 )/( 2)}x`

Figure 2 shows ƒ(x) (purple) and g(x) = -ƒ(x) (black).