Adding and subtracting big polynomials like these are pretty easy. You just need to combine like terms. For example:
1.)
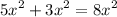
2.)
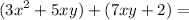
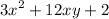
(The 3x^2 and the 2 stay intact while the 5xy and 7xy combine together)
All you have to do is combine the numbers that have the same powers of x and y with each other. x^2 will combine with x^2 and xy^2 wil combine with xy^2 exc. If there is no other number with the same x and y's, then you just leave it as it is in the answer.
Now with the original question, I see a -9xy^3, and thats gonna combine with the 3xy^3 in the second polynomial and the 2xy^3 in the third one.
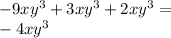
So far we have -4xy^3, the next term is going to be a -9x^4y^3, and that's gonna combine with the 3x^4y^3 in the third one.
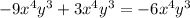
We now finished adding the like terms that were in the first polynomial, we will move onto the second polynomial. The first term in this one is 3xy^3, in which we already added in the first step. At this point, it doesn't look like there are any other terms that have the same x and y behind them. So we can move on and write the final answer:
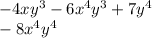
(All on the same line of course)
Also, for your second question, the order does not matter in which you write the terms. I could write the 7y^4 behind the -8x^4y^4 and it would still be the same answer.
If you have any other questions let me know :) while I double check my work.