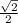Question

Use the unit circle to find cos Θ.

Note: Attachment and answer choices regarded to question

Answer 1

`(√(2))/(2)`

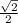
Explanation:

Start by determining the simpler angle
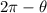`2\pi-\theta` (or, the complement of the highlighted angle in red on your image). The cosine of that angle is

`\cos (2\pi-\theta) = (x)/(1)=((√(2))/(2))/(1)=(√(2))/(2)`

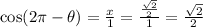
Now, back to the actual red-circled angle. That one is going in the negative direction and ends up in the same position on the unit circle. Since cosine is an even function, its value is the same whether you evaluate at an angle theta, or its complement 2pi-theta. So, the final answer is:
`(√(2))/(2)`

Answer 2

C) (√2)/2

Explanation:

The cosine of the angle is the x-coordinate of the terminal ray's intersection with the unit circle. That is clearly shown as (√2)/2. (It does not matter how you get there, as long as the angle is measured from the +x axis.)