Answer: Options A and C.
Explanation:
The parent exponential function has the form:
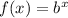
This can be transformated as following:
When you multiply the function by a factor a (
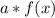 ) and a>0 , then the function is vertically stretched.
) and a>0 , then the function is vertically stretched.
When you add a number k to the parent function, the function is shifted up (
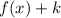 )
)
The parent function given in the problem is:
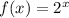
To obtain the function
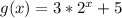 , the parent function is multiplied by a factor 3 (which is greater than 0) and the number 5 is added.
, the parent function is multiplied by a factor 3 (which is greater than 0) and the number 5 is added.
Therefore, the graph is shifted up and vertically stretched.