Question

Suppose that a regression line for some data transformed with logarithms predicts that when x equals 6, log(y) will equal 2.012. What does the regression line predict y will equal when x equals 6?

Answer 1

Answer: The regression line predicts that at x = 6, the value of y = 102.80.

Explanation:

Since we have given that

When x = 6,

`\log y=2.012`

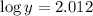
We need to find the value of 'y' when x=6:

`\log_(10)y=2.012`

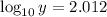
Since it is logarithmic function with base 10.

So, it becomes,

`\log_(10)y=2.012\\\\y=10^(2.012)\\\\y=102.80`

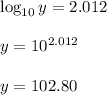
Hence, The regression line predicts that at x = 6, the value of y = 102.80.

Answer 2

102.8

Explanation:

If log₁₀y = 2.012, y = 10^2.012 = 102.8