Answer:
Explanation:
The method you use is sort of a chain rule when you hit a y. Here's what I get
d(x^3)/dx = 3x^2
d(y^2)/dx = 2y * (dy/dx) This is where the chain rule comes in.
-d(2xy)/dy = -2y - 2x dy/dx
d(2)/dx = 0 Two is a constant. Its derivative = 0.
Now add these together.
3x^2 + 2y*(dy/dx) - 2y - 2x*(dy/dx) = 0
Now group the terms not containing dy/dx
3x^2 - 2y
And then group those containing dy/dx
2y (dy/dx) - 2x (dy/dx)
Pull out the common factor 2[dy/dx]
2 (dy/dx) [y - x]
Put the non dy/dx terms on the right
2(dy/dx) ( y + x) = - (3x^2 + 2y)
Divide both sides by 2(y - x)
(dy/dx) =
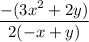
You have the tangent expression. dy/dx is one expression for the tangent. The other is the fraction on the right.
You are almost home free.
Let x = - 1
Let y = 1
dy/dx = -(3(-1)^2 + 2(1) ) / (2(1 + 1)
dy/dx = -(3 + 2) /(2*2)
dy/dx = - (5)/4
dy/dx = - 1.25
Check my numbers pretty carefully. The method is correct. There are so many lines that the answer may not be.