The rule for deriving a multiplication is
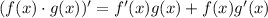
Also, we can forget about the factor 4 for now, since we have

So, we will just multiply everything by 4 at the end. Our functions are
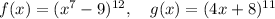
For both derivatives we will use the rule
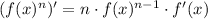
So, we have
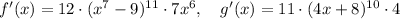
We can simplify those expression a little bit:
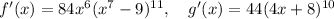
The formula
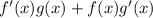 thus becomes
thus becomes
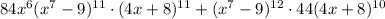
And so the final answer is
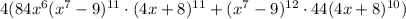
If you simplify this expression by factoring common terms, you will see that the correct answer is the first one.