Question

If a polynomial function f(x) has roots 0 ,4, and 3+ 11, what must also be a root of f(x)

Answer 1

3-√11

Explanation:

If a polynomal function f(x) has roots 0, 4 and 3+√11, then 3-√11 must be also a root of f(x).

Probably, we are in front of a four degree polynomial. The first two roots were found, and then the last root was found using the quadratic formula, which states that for a polynomial of the time
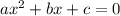`ax^(2) +bx + c = 0`. The roots are given by:

`x1 = \frac{-b+\sqrt{b^(2)-4ac } }{2a}`

`x2 = \frac{-b-\sqrt{b^(2)-4ac } }{2a}`

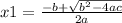
We have that one root is 3+√11, therefore the other one should be 3-√11.