Answer:
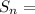 -348
-348
Explanation:
We are given the following arithmetic sequence and we are to find the sum of its first 12 terms:
1, -4, -9, -14, . . .
For that, we will use the formula for the sum of the arithmetic mean:
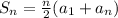
We know the value of the first term (
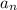 ) but we need to find the value of
) but we need to find the value of
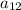 . So we will use the following formula:
. So we will use the following formula:
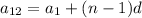
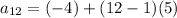
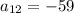
Substituting these values in the sum formula to get:
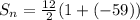
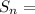 -348
-348