Answer:
8.85% per year
Explanation:
To find the interest rate of a compounding interest, we use the formula:
![r=n[((A)/(P))^{(1)/(nt)}-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z8oq7xh9wft6ijsu7hc2c0d3yat1twqaa3.png)
Before we start solving, let's break down all the variables that we have.
A = 19,992.71
P = 10,000.00
n = 2
t = 8
r = ?
Now let's put the values into the formula.
![r=2[((19,992.71)/(10,000.00))^{(1)/(2(8))}-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mapams8jzujt5wigigogbhqgilmxfo85n3.png)
![r=2[((19,992.71)/(10,000.00))^{(1)/(16)}-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/calx8k7foq8gy5wcmwvtzfjr39o4bvok4u.png)
![r=2[((19,992.71)/(10,000.00))^(0.0625)-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fyv8glsm4nurfzvowh7hjnf26k4v3aqqfy.png)
![r=2[(1.9992.1)^(0.0625)-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nsli36hvgqcktqgmbg3x0x3c5vhosjxlk7.png)
![r=2[1.0442499885-1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/etxbpq4jb0mus2xskocudv1j24lqfc6thj.png)
![r=2[0.0442499885]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2fr15pd79k6a1edesznsbq9w9jlberd9f6.png)
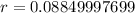 or
or
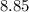
So the rate the Mrs. Emily Francis got from the bank was 8.85% per year.