1.31 × 10⁴ grams.
Step-by-step explanation
Assume that oxygen acts like an ideal gas. In other words, assume that the oxygen here satisfies the ideal gas law:
 ,
,
where
 the pressure on the gas,
the pressure on the gas,
 ;
;
 the volume of the gas,
the volume of the gas,
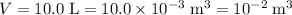 ;
;
 the number of moles of the gas, which needs to be found;
the number of moles of the gas, which needs to be found;
 the absolute temperature of the gas,
the absolute temperature of the gas,
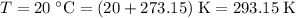 .
.
 the ideal gas constant,
the ideal gas constant,
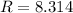 if P, V, and T are in their corresponding SI units: Pa, m³, and K.
if P, V, and T are in their corresponding SI units: Pa, m³, and K.
Apply the ideal gas law to find
 :
:
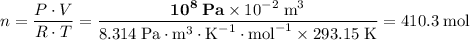 .
.
In other words, there are 410.3 moles of O₂ molecules in that container.
There are two oxygen atoms in each O₂ molecules. The mass of mole of O₂ molecules will be
 . The mass of 410.3 moles of O₂ will be:
. The mass of 410.3 moles of O₂ will be:
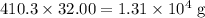 .
.
What would be the mass of oxygen in the container if the pressure is approximately the same as STP at
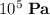 or
or
 instead?
instead?