Answer:
437mm²
Explanation:
First we need to find the total area of the rectangle. The area of a rectangle can be found by using the formula:
A = L x W
L = 15mm
W = 38mm
So now we plug it into our formula.
A = 15mm x 38mm
A = 570mm²
Now that we have the total area, we now need to solve for the area of the triangle.
The area of a triangle can be found by using the formula:
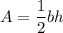
To find the height of the triangle we take the total height and subtract it to the measurement given in the figure.
h = 15mm - 8mm
h = 7mm
b = 38mm
Now that we have both the base and height we can use the formula for the triangle.
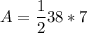
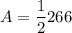
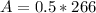
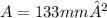
Now that we have the area of both the triangle and the rectangle, we simply subtract the area of the triangle to the area of the rectangle.
Shaded Area = 570mm² - 133mm²
Shaded Area = 437mm²
The area of the shaded area is equal to 437mm².