Question

Raft 16 miles with river current.at end of 16 miles turns around and rafts against river current. overall the journey takes 4 hours he can raft 9 mph in still water. what is speed of current

Answer 1

Let the speed of the current of the river be = x

And, the speed of the boat in still water = 9 mph

Then, the speed of boat along the river current will be= 9+x mph

And, speed of boat against the river current will be = 9-x mph

Now as given, total distance along river current and total distance against river current is same = 16 miles.

As we know, time=distance/speed

Time taken by boat along the river current =
`(16)/(9+x)`

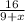
And time taken by boat against the river current =
`(16)/(9-x)`

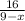
Also given is , the overall the journey takes 4 hours; so equation becomes

`(16)/(9+x)+(16)/(9-x)=4`

`4((1)/(9+x)+(1)/(9-x))=1`

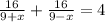
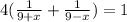
Solving this we get;
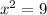`x^(2) =9` or x=3

Therefore, the speed of the current of the river is 3 mph.